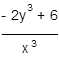IFoA IFoA_CAA_M0 - Module 0 - Entry Exam
The random variable X has the following probability density function ("PDF"):
Â
 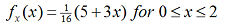
Â
 Calculate: P(x ≥ 1.5)
State what the limit of a function with input variable x represents.
Using simple iteration, based on trial and improvement, the cubic equation below can be solved:
2x3Â + 5x2Â +7x - 12 = 0Â
Â
Solve for x to 6 decimal places.
In a small island nation, local sea vessels are identified using "a letter and 4 digits" classification system. The "letter" can be any of the 26 letters in the English alphabet, A to Z, Â while the "digit" can be any number from 0 to 9. E.g: Z9835.
Â
Calculate the probability of a sea vessel having an identification ending in "007".
Identify which of the following statements are true.
Â
I. Skewness measures how peaked a set of data is.
II. Skewness is a measure of asymmetry of the distribution of the data about its mean.
III. For a symmetrically distributed data, the mean equals the median but not necessarily the mode.
IV. The value of a measure of skewness can be positive, zero or negative.
A boy is asked to estimate the height of his sister. He estimates that she is 1.60 metres tall. He then measures his sister and finds that her true height is 1.40 metres.
Â
Identify the absolute error of his estimate of her height.
A geometric series is given by
Â
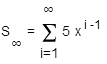
Â
 Identify the values of x for which the series converges.
Consider a function f which has three variables, x1, x2 and x3.
Â
Identify which of the following gives a correct definition of a partial derivative of the function f.
If
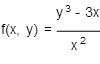
Calculate the partial derivative
A)
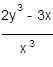
B)
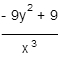
C)
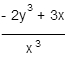
D)