Summer Sale Limited Time 65% Discount Offer - Ends in 0d 00h 00m 00s - Coupon code: ecus65

IFoA IFoA_CAA_M0 - Module 0 - Entry Exam

IFoA IFoA_CAA_M0 Premium Access     Download Demo    
Page: 1 / 2
Total 64 questions

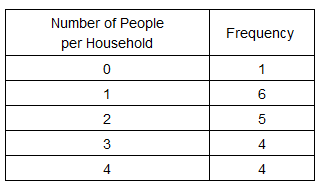
The table below shows the distribution of the number of people in each household in a village.

 

 

Determine which of the following inequalities is true for the number of people living in a house.

A.

Mode < Median < Mean

B.

Mode < Mean < Median

C.

Median < Mean < Mode

D.

Median < Mode < Mean

Determine which of the statements is true about the root(s) of the following equation:

 

A.

There is only one real root which takes a positive value.

B.

There is only one real root which takes a negative value.

C.

There are two real roots, r1 and r2, where r1 is positive and:

r1 = - 0.5 r2

D.

There are two real roots, r1 and r2, where r1 is positive and:

r1 = - 2 r2

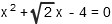
An insurance company sells policies where, for each policy, the policyholder pays the first £50 of the cost of any claim. A claim reported to the insurance company takes some unknown value £x.

 

Identify which of the mathematical expressions below represents the cost in £ to the insurance company of the claim.

A.

x - 50

B.

x

C.

max(x, 50)

D.

max(x - 50, 0)

Calculate the total area enclosed by the x-axis and the function below, between x = 1.5 and x = 2.

f(x) = 2x3

A.

2.734

B.

5.469

C.

8.000

D.

10.938

An individual purchases a share in a company at a price of £45. Six months later he sells the share for £39.

 

Calculate the percentage change in the value of the share over the six month period, correct to one decimal place.

A.

-15.4%

B.

-13.3% 

C.

13.3%

D.

86.7%

The graph shows the frequency distribution of the age of people with a certain kind of insurance contract.

 

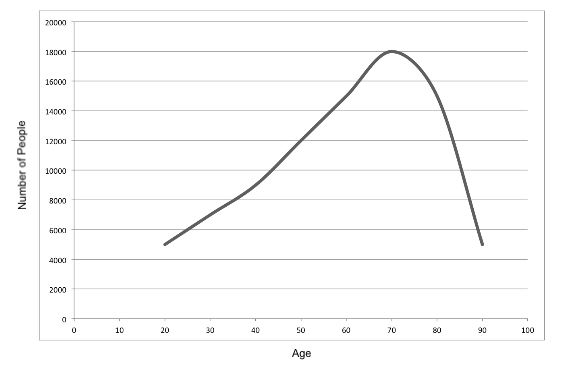
Describe the shape of the underlying data.

A.

Negatively skewed

B.

Positively skewed

C.

Symmetric

D.

Symmetric about the mean

Determine and describe the extreme values of f(x,y) = -x2 - xy - 3y2

A.

(0,1) and a saddle point

B.

(0,0) and a minimum

C.

(0,0) and a maximum

D.

(0.5,-1) and a maximum

Integrate:

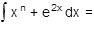
A)

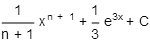
B)

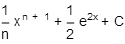
C)

D)

A.

Option A

B.

Option B

C.

Option C

D.

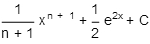
Option D

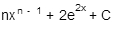
Consider the vector U = (3, -1, 5).

 

Calculate the magnitude of vector U to two decimal places.

A.

2.65

B.

5.92

C.

7.00

D.

9.00

The variable s can take values between 2 and 6.

 

Identify which of the inequalities shown can be satisfied by at least one value of s.

A.

s + 5 < 6

B.

s + 9 < 6

C.

s - 6 > 2

D.

s - 2 > 2